This post will guide you through developing your very own trading algorithm in QuantConnect. A familiarity in C# and basic finance knowledge is assumed, but I’ll be gentle — promise! Already an expert? Skip to the code.
More comfortable with Python? View the alternate tutorial.
The algorithm we’ll build is based on the principle of a proportionated simple moving average (P-SMA). We will choose a benchmark (SPY in this example) and, based on its simple moving average, decide if the market will go up or down. If we predict the market will go up, we will invest in equities that provide fast growth but increased risk. Otherwise, we invest in safe assets, such as treasury bonds. Proportionated means the decision is not binary. For example, we may calculate 30% of our portfolio should be relatively risk-less and allocate 70% for high growth equities.
Time to code! Any algorithm in QuantConnect starts the same way:
namespace QuantConnect.Algorithm.CSharp{
public class ProportionalSimpleMovingAverage : QCAlgorithm{
public override void Initialize(){
return;
}
}
}
First, we instantiate the class. The name can be anything you like, but it’s important to extend QCAlgorithm. Whenever an algorithm is started, Initialize is called exactly once and allows us to setup the properties of our algorithm. First, we’ll define some member variables. This should go immediately before Initialize, inside the class.
...
private static Symbol _spy
= QuantConnect
.Symbol.Create("SPY", SecurityType
.Equity, Market
.USA);
private static Symbol _qqq
= QuantConnect
.Symbol.Create("QQQ", SecurityType
.Equity, Market
.USA);
private static Symbol _tlt
= QuantConnect
.Symbol.Create("TLT", SecurityType
.Equity, Market
.USA);
private static Symbol _agg
= QuantConnect
.Symbol.Create("AGG", SecurityType
.Equity, Market
.USA);
private Symbol _benchmark
= _spy
;
private List
<Symbol
> _risk_on_symbols
= new List
<Symbol
>{
_spy,
_qqq
};
private List
<Symbol
> _risk_off_symbols
= new List
<Symbol
>{
_tlt,
_agg
};
private RollingWindow
<decimal> _close_window
;
public override void Initialize
(){
... When coding in C#, a common convention is to denote member variables with an underscore. The first four lines create the “symbol”, a reference to specify the desired equity. Next, we define our “benchmark”. This is the equity that will be used as the basis for all future calculations. Moving on to the lists: remember, we want to invest in either high growth or low risk assets depending on the market. _risk_on_symbols will be invested when we want to add risk to our portfolio — predicting an upswing. _risk_off_symbols are our low risk investments. You should feel free to experiment with different symbols. You can add as many or as few equities as you like to either list. The final member variable is_close_window. This is a rolling window — a special list that will only keep a fixed number of the most recent elements. Specifically, we’ll be using a window size of 84, and storing decimal numbers (daily closing price of the benchmark equity); because the window is not static, we declare it here but instantiate the window later inside the Initialize method.
Let’s begin to flesh out initialize.
public override void Initialize(){
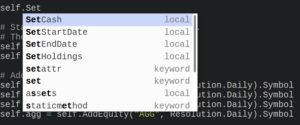
SetStartDate(2016, 01, 01);
SetEndDate(2016, 10, 14);
SetCash(10000);
AddEquity(_spy, Resolution.Daily);
AddEquity(_qqq, Resolution.Daily);
AddEquity(_tlt, Resolution.Daily);
AddEquity(_agg, Resolution.Daily);
}
Methods such as SetCash, SetStartDate, and SetEndDate are only applicable when running a back-test. They are completely ignored during live trading.
AddEquity is essential to any algorithm. By adding the equity in the initialize method, the relevant information will be made available throughout the algorithm. Resolution.Daily specifies data will be given with a daily window. Other options are tick, second, minute, and hour.
_close_window
= new RollingWindow
<decimal>(84);
IEnumerable
<TradeBar
> slices
= History
(_benchmark,
84);
foreach(TradeBar bar
in slices
){
_close_window
.Add(bar
.Close);
}The code here is responsible for initializing the rolling window. The first line creates the window and sets the type and size to decimal and 84 respectively. Next the History function is called to get historical information about the benchmark during the last 84 days. Finally, we loop through every day of historic data and add the closing price to the rolling window. This ensures the algorithm will always have 84 days of information to use for calculations.
Schedule.On(DateRules.EveryDay(_benchmark),
TimeRules.AfterMarketOpen(_benchmark, 10),
EveryDayOnMarketOpen);
The snippet above will complete our Initialize method. This is the main driver of your algorithm. It schedules a method called EveryDayOnMarketOpen to run every day that SPY (the benchmark) is trading, 10 minutes after market open.
Next, we build a simple function to assist with calculating averages over various window sizes.
private decimal GetRollingAverage(int n, RollingWindow<decimal> window){
decimal sum = 0;
for (int i = 0; i < n; i++){
sum += window[i];
}
return sum / n;
}
This function accepts two parameters, an integer n denotes the number of days to look back, and a RollingWindow over which to do the averaging. The for loop will iterate through the window until it reaches the nth entry. At that point, the sum will be divided by n and the simple average will be returned.
Since setup is over with, let’s move on to the heart of the algorithm by defining EveryDayOnMarketOpen.
public void EveryDayOnMarketOpen(){
if (Transactions.GetOpenOrders().Count > 0){
return;
}
}
Nothing groundbreaking here. We just return immediately if there are any open orders. In theory, this should never happen. Our algorithm will submit market orders 10 minutes after market open, and is run once per trading day. If this block does execute, it’s likely an indicator of a more serious, underlying problem. Nevertheless, better safe than sorry.
IEnumerable<TradeBar> slices = History(_benchmark, 1);
TradeBar last_bar = slices.Last();
decimal bench_close = last_bar.Close;
_close_window.Add(bench_close);
decimal bench_mean_short = GetRollingAverage(21, _close_window);
decimal bench_mean_long = GetRollingAverage(84, _close_window);
The History method returns TradeBars, representing data on the specified equity. We use the History function to get yesterday’s closing price and add it to the rolling window. The final two lines calculate the average closing price over the specified period. Our algorithm compares moving averages over two different window sizes, 21 and 84 days. These are arbitrary (but common) intervals. I encourage you to experiment by changing these values. Note that if you want to look back past 84 days the rolling window size will need to be increased in the Initialize function. QuantConnect does offer convenience methods to calculate various indicators to use in your projects, which makes code easier to read.
decimal risk_on_pct = (bench_mean_short / bench_close) *
((bench_mean_short * 2m / bench_mean_long) * .25m) /
_risk_on_symbols.Count;
decimal risk_off_pct = (bench_close / bench_mean_short) *
((bench_mean_long * 2m / bench_mean_short) * .25m) /
_risk_off_symbols.Count;
foreach (Symbol sid in _risk_on_symbols){
SetHoldings(sid, risk_on_pct);
}
foreach (Symbol sid in _risk_off_symbols){
SetHoldings(sid, risk_off_pct);
}
Finally, the exciting stuff! The “risk on” and “risk off” percentages are calculated using our history data. SetHoldings will allocate a percentage of your portfolio to the specified equity. For instance, SetHoldings(_spy, 1) will buy as much SPY as you can afford, 100% of your portfolio. If you have a margin account and want to leverage your position, simply allocate more than 100%. SetHoldings(_spy, 2) will buy twice as many SPY shares as you can actually afford.
That’s it! You now have an algorithm that can trade automatically on your behalf. I encourage you to experiment changing/improving the algorithm on your own.
This example is also available on GitHub.