Tag: tutorial

Jupyter Notebook: Getting Started and Installation

Jupyter Notebook provides a simple way to run code in Python, R, Scala and more. While it’s mainly used in research related fields, Jupyter can be applied to a wide variety of applications.

Jupyter is especially useful for two groups in particular. Data scientists and machine learning experts benefit from modular execution. They can load a large data set once and try many different experiments/code changes; saving an enormous amount of time in the process. Academics make up the other group. Documenting work as you go could not be easier. Professors can auto grade students work using tools like Vocareum, built to work with Jupyter.

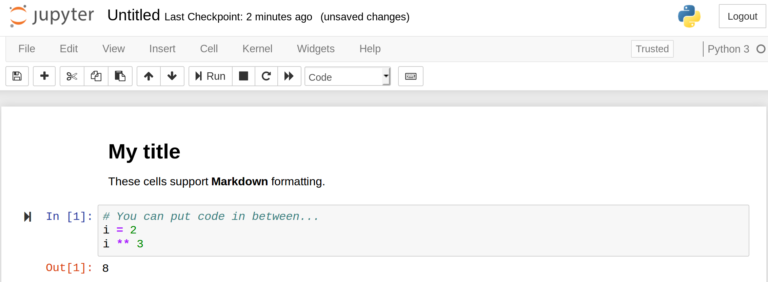
Above is a screenshot directly from a notebook. It runs in a web interface and is quite easy to use. Markdown syntax can be added to create documentation blocks — much more expressive than the brief inline comments we programmers often get used to.

Installing Jupyter Notebook

Some prefer the native installation while others like to keep everything in a self-contained Docker container. I will outline both methods — choose the one that works best for you.

Native

Jupyter Notebook is easy to install with pip. I assume you already have Python and pip installed. If that’s the case, simply run

python3 -m pip install jupyter #for Python3
python -m pip install jupyter  #for Python2

Congratulations, that’s it! To run Jupyter, simply open up a new terminal in the directory you want the notebooks to be saved. Then type:

jupyter notebook

Your default browser should automatically open to the Jupyter instance.

Docker

This guide assumes Docker is already installed. If you’re unfamiliar with Docker, please check out their guide.

Using Jupyter with Docker is easy, a container is already maintained. Simply run the container with the following command:

docker run -it -v /path/to/jupyter/directory:/work --net=host --rm jupyter/all-spark-notebook

The -v flag is used to share a local directory with Docker. /path/to/jupyter/directory should point to a local directory where you want the notebooks to be saved. When inside the Jupyter instance, be sure to save everything inside the /work directory, or it will not be saved.

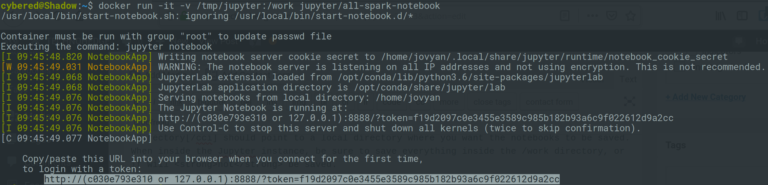
Once the Docker container is launched, a unique URL will be printed to the console. Copy and paste that into a web browser and you’re good to go! You may notice the example below says 127.0.0.1 or a seemingly random string of numbers. If this is the case for you, be sure to substitute 127.0.0.1. For instance, open a web browser and go directly to the URL http://127.0.0.1:8888/?token=f19d2097c0e3455e3589c985b182b93a6c9f022612d9a2cc. Your token will be different!

Your first Jupyter project

With Jupyter successfully installed, your screen should be similar to the one pictured below.

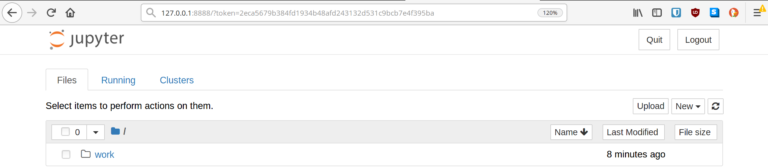
Once Jupyter Notebook is installed and launched, we can create our first actual notebook. If you installed with Docker, be sure to click on the work directory first. Then click the New dropdown, then select Python 3 (or a different language if you prefer).

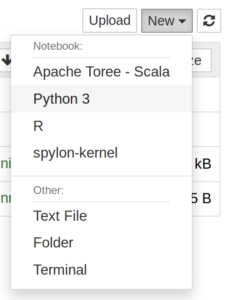
All that remains is filling it with content. Each content block is a cell. There are two main types of cells: code and Markdown.

Let’s create a new code cell.

Run the code in a cell by clicking the play button with the cell selected, or by hitting ctrl + enter on the keyboard.

Now, let’s demonstrate one of the main benefits of Jupyter. Say we need to load data, which takes a lot of time. If this was a standard Python script, the data would have to be loaded during each subsequent run. This is not the case with Jupyter. We can simply put the data loading code into its own cell.

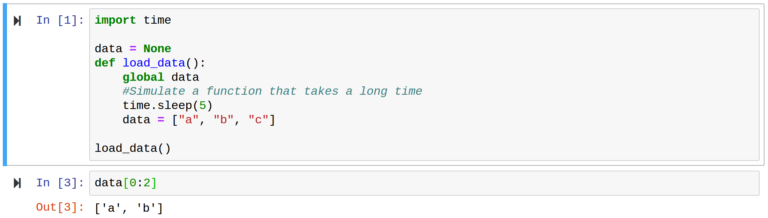
Saving & Checkpoints

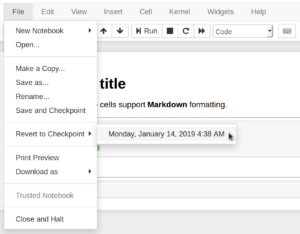
To save your work, simply click the Save & Checkpoint button.

As the name suggests, manually saving also creates a checkpoint. Checkpoints are a form of basic version control — you can easily roll back to any checkpoint later on. Work in a notebook will also be periodically auto-saved, but checkpoints must be created manually.

To share your work with someone else, simply send them the .ipynb file. They can launch the file using their own Jupyter installation and pick up right where you left off. While you can use Jupyter with a version control system (like Git of Mercurial) by checking in the .ipynb files, it’s not easy to see the individual code changes later. This is my single biggest complaint when using Jupyter. If anyone has found a solution, I would love to hear it!

Posted on by Edward Atter 2

Building your first algorithm in QuantConnect (Python)

This post will guide you through developing your very own trading algorithm in QuantConnect. A familiarity in python and basic finance knowledge is assumed, but I’ll be gentle — promise! Already an expert? Skip to the code.

More comfortable with C#? View the alternate tutorial.

The algorithm we’ll build is based on the principle of a proportionated simple moving average (P-SMA). We will choose a benchmark (SPY in this example) and, based on its simple moving average, decide if the market will go up or down. If we predict the market will go up, we will invest in equities that provide fast growth but increased risk. Otherwise, we invest in safe assets, such as treasury bonds. Proportionated means the decision is not binary. For example, we may calculate 30% of our portfolio should be relatively risk-less and allocate 70% for high growth equities.

Time to code! Any algorithm in QuantConnect starts the same way:

class ProportionalSMAFast(QCAlgorithm):
    def Initialize(self):
        pass

First, we instantiate the class. The name can be anything you like, but it’s important to extend QCAlgorithm. Whenever an algorithm is started, Initialize is called exactly once and allows us to setup the properties of our algorithm. Let’s begin to flesh out initialize.

def Initialize(self):
    self.SetCash(10000)

    self.SetStartDate(2016,01,01)
    self.SetEndDate(2016,10,14)

    # Add all assets you plan on using later
    self.spy = self.AddEquity("SPY", Resolution.Daily).Symbol
    self.qqq = self.AddEquity("QQQ", Resolution.Daily).Symbol
    self.tlt = self.AddEquity("TLT", Resolution.Daily).Symbol
    self.agg = self.AddEquity("AGG", Resolution.Daily).Symbol

    self.benchmark = self.spy

    self.risk_on_symbols = [self.spy, self.qqq]
    self.risk_off_symbols = [self.tlt, self.agg]

Methods such as SetCash, SetStartDate, and SetEndDate are only applicable when running a back-test. They are completely ignored during live trading.

AddEquity is essential to any algorithm you write. By adding the equity in the initialize method, the relevant equity data will be made available throughout your algorithm. Resolution.Daily specifies data will be given with a daily window. Other options are tick, second, minute, and hour.

So what about the .Symbol and self.my_equity? Why assign the variable? This is not strictly necessary. Specifically, the following code is all that is required to make the equity data available.

self.AddEquity("SPY", Resolution.Daily)

By assigning self.spy, we can prevent hard coding the string "SPY" everywhere and use the variable instead. If you’re a little confused about this point, don’t worry. It will become more apparent later on.

And the final two lines? Remember, we want to invest in either high growth or low risk assets depending on the market. risk_on_symbols will be invested when we want to add risk to our portfolio — predicting an upswing. risk_off_symbols are our low risk investments. You should feel free to experiment with different symbols. You can add as many or as few equities as you like to either list.

#Schedule every day SPY is trading
self.Schedule.On(self.DateRules.EveryDay(), \
                 self.TimeRules.AfterMarketOpen(self.benchmark, 10), \
                 Action(self.EveryDayOnMarketOpen))

The snippet above will complete our Initialize method. This is the main driver of your algorithm. It schedules a method called EveryDayOnMarketOpen to run every day that SPY (our benchmark) is trading, 10 minutes after market open.

Since setup is over with, let’s move on to the heart of the algorithm by defining EveryDayOnMarketOpen.

def EveryDayOnMarketOpen(self):
    #Do nothing if outstanding orders exist
    if self.Transactions.GetOpenOrders():
        return

Nothing groundbreaking here. We just return immediately if there are any open orders. In theory, this should never happen. Our algorithm will submit market orders 10 minutes after market open, and is run once per trading day. If this block does execute, it’s likely an indicator of a more serious, underlying problem. Nevertheless, better safe than sorry.

#Lookup last 84 days
slices = self.History(self.spy, 84)
#Get close of last (yesterday's) slice
spy_close = slices["close"][-1]

#Get mean over last 21 days
spy_prices_short = slices["close"][-21:]
spy_mean_short = spy_prices_short.mean()

#Get mean over last 84 days
spy_prices_long = slices["close"]
spy_mean_long = spy_prices_long.mean()

The self.History method returns a pandas data frame, representing data on the specified equity for the previous 84 days. Our algorithm compares moving averages over two different window sizes, 21 and 84 days. These are arbitrary (but common) intervals. I encourage you to experiment by changing these values. The next two blocks splice the last 21 and 84 closing prices from the data frame and calculate the average.

risk_on_pct  = (spy_mean_short/spy_close) * \
               ((spy_mean_short *2 / spy_mean_long) *.25) / \
               len(self.risk_on_symbols)
risk_off_pct = (spy_close/spy_mean_short) * \
               ((spy_mean_long *2 / spy_mean_short) *.25) / \
               len(self.risk_off_symbols)

#Submit orders
for sid in self.risk_on_symbols:
    self.SetHoldings(sid, risk_on_pct)
for sid in self.risk_off_symbols:
    self.SetHoldings(sid, risk_off_pct)

Finally, the exciting stuff! The “risk on” and “risk off” percentages are calculated using our history data. self.SetHoldings will allocate a percentage of your portfolio to the specified equity. For instance, self.SetHoldings("SPY", 1) will buy as much SPY as you can afford, 100% of your portfolio. If you have a margin account and want to leverage your position, simply allocate more than 100%. self.SetHoldings("SPY", 2) will buy twice as many SPY shares as you can actually afford.

That’s it! You now have an algorithm that can trade automatically on your behalf. I encourage you to experiment changing/improving the algorithm on your own.

This example is also available on GitHub.

Posted on by Edward Atter 3

Building your first algorithm in QuantConnect (C#)

This post will guide you through developing your very own trading algorithm in QuantConnect. A familiarity in C# and basic finance knowledge is assumed, but I’ll be gentle — promise! Already an expert? Skip to the code.

More comfortable with Python? View the alternate tutorial.

The algorithm we’ll build is based on the principle of a proportionated simple moving average (P-SMA). We will choose a benchmark (SPY in this example) and, based on its simple moving average, decide if the market will go up or down. If we predict the market will go up, we will invest in equities that provide fast growth but increased risk. Otherwise, we invest in safe assets, such as treasury bonds. Proportionated means the decision is not binary. For example, we may calculate 30% of our portfolio should be relatively risk-less and allocate 70% for high growth equities.

Time to code! Any algorithm in QuantConnect starts the same way:

namespace QuantConnect.Algorithm.CSharp{
    public class ProportionalSimpleMovingAverage : QCAlgorithm{
        public override void Initialize(){
            return;
        }
    }
}

First, we instantiate the class. The name can be anything you like, but it’s important to extend QCAlgorithm. Whenever an algorithm is started, Initialize is called exactly once and allows us to setup the properties of our algorithm. First, we’ll define some member variables. This should go immediately before Initialize, inside the class.

...
private static Symbol _spy = QuantConnect.Symbol.Create("SPY", SecurityType.Equity, Market.USA);
private static Symbol _qqq = QuantConnect.Symbol.Create("QQQ", SecurityType.Equity, Market.USA);
private static Symbol _tlt = QuantConnect.Symbol.Create("TLT", SecurityType.Equity, Market.USA);
private static Symbol _agg = QuantConnect.Symbol.Create("AGG", SecurityType.Equity, Market.USA);
   
private Symbol _benchmark = _spy;
   
private List<Symbol> _risk_on_symbols = new List<Symbol>{
    _spy,
    _qqq
};  
private List<Symbol> _risk_off_symbols = new List<Symbol>{
    _tlt,
    _agg
};  
   
private RollingWindow<decimal> _close_window;

public override void Initialize(){
    ...

When coding in C#, a common convention is to denote member variables with an underscore. The first four lines create the “symbol”, a reference to specify the desired equity. Next, we define our “benchmark”. This is the equity that will be used as the basis for all future calculations. Moving on to the lists: remember, we want to invest in either high growth or low risk assets depending on the market. _risk_on_symbols will be invested when we want to add risk to our portfolio — predicting an upswing. _risk_off_symbols are our low risk investments. You should feel free to experiment with different symbols. You can add as many or as few equities as you like to either list. The final member variable is_close_window. This is a rolling window — a special list that will only keep a fixed number of the most recent elements. Specifically, we’ll be using a window size of 84, and storing decimal numbers (daily closing price of the benchmark equity); because the window is not static, we declare it here but instantiate the window later inside the Initialize method.

Let’s begin to flesh out initialize.

public override void Initialize(){
    SetStartDate(2016, 01, 01);
    SetEndDate(2016, 10, 14);
    SetCash(10000);

    AddEquity(_spy, Resolution.Daily);
    AddEquity(_qqq, Resolution.Daily);
    AddEquity(_tlt, Resolution.Daily);
    AddEquity(_agg, Resolution.Daily);
}

Methods such as SetCash, SetStartDate, and SetEndDate are only applicable when running a back-test. They are completely ignored during live trading.

AddEquity is essential to any algorithm. By adding the equity in the initialize method, the relevant information will be made available throughout the algorithm. Resolution.Daily specifies data will be given with a daily window. Other options are tick, second, minute, and hour.

_close_window = new RollingWindow<decimal>(84);
IEnumerable<TradeBar> slices = History(_benchmark, 84);
foreach(TradeBar bar in slices){
    _close_window.Add(bar.Close);
}

The code here is responsible for initializing the rolling window. The first line creates the window and sets the type and size to decimal and 84 respectively. Next the History function is called to get historical information about the benchmark during the last 84 days. Finally, we loop through every day of historic data and add the closing price to the rolling window. This ensures the algorithm will always have 84 days of information to use for calculations.

Schedule.On(DateRules.EveryDay(_benchmark),
        TimeRules.AfterMarketOpen(_benchmark, 10),
        EveryDayOnMarketOpen);

The snippet above will complete our Initialize method. This is the main driver of your algorithm. It schedules a method called EveryDayOnMarketOpen to run every day that SPY (the benchmark) is trading, 10 minutes after market open.

Next, we build a simple function to assist with calculating averages over various window sizes.

private decimal GetRollingAverage(int n, RollingWindow<decimal> window){
    decimal sum = 0;
    for (int i = 0; i < n; i++){
        sum += window[i];
    }  
       
    return sum / n;
}

This function accepts two parameters, an integer n denotes the number of days to look back, and a RollingWindow over which to do the averaging. The for loop will iterate through the window until it reaches the nth entry. At that point, the sum will be divided by n and the simple average will be returned.

Since setup is over with, let’s move on to the heart of the algorithm by defining EveryDayOnMarketOpen.

public void EveryDayOnMarketOpen(){
    if (Transactions.GetOpenOrders().Count > 0){
        return;
    }  
}

Nothing groundbreaking here. We just return immediately if there are any open orders. In theory, this should never happen. Our algorithm will submit market orders 10 minutes after market open, and is run once per trading day. If this block does execute, it’s likely an indicator of a more serious, underlying problem. Nevertheless, better safe than sorry.

IEnumerable<TradeBar> slices = History(_benchmark, 1);
TradeBar last_bar = slices.Last();
decimal bench_close = last_bar.Close;
       
_close_window.Add(bench_close);
       
decimal bench_mean_short = GetRollingAverage(21, _close_window);
decimal bench_mean_long = GetRollingAverage(84, _close_window);

The History method returns TradeBars, representing data on the specified equity. We use the History function to get yesterday’s closing price and add it to the rolling window. The final two lines calculate the average closing price over the specified period. Our algorithm compares moving averages over two different window sizes, 21 and 84 days. These are arbitrary (but common) intervals. I encourage you to experiment by changing these values. Note that if you want to look back past 84 days the rolling window size will need to be increased in the Initialize function. QuantConnect does offer convenience methods to calculate various indicators to use in your projects, which makes code easier to read.

decimal risk_on_pct = (bench_mean_short / bench_close) *
                        ((bench_mean_short * 2m / bench_mean_long) * .25m) /
                        _risk_on_symbols.Count;
decimal risk_off_pct = (bench_close / bench_mean_short) *
                        ((bench_mean_long * 2m / bench_mean_short) * .25m) /
                        _risk_off_symbols.Count;

foreach (Symbol sid in _risk_on_symbols){
    SetHoldings(sid, risk_on_pct);
}  
foreach (Symbol sid in _risk_off_symbols){
    SetHoldings(sid, risk_off_pct);
}

Finally, the exciting stuff! The “risk on” and “risk off” percentages are calculated using our history data. SetHoldings will allocate a percentage of your portfolio to the specified equity. For instance, SetHoldings(_spy, 1) will buy as much SPY as you can afford, 100% of your portfolio. If you have a margin account and want to leverage your position, simply allocate more than 100%. SetHoldings(_spy, 2) will buy twice as many SPY shares as you can actually afford.

That’s it! You now have an algorithm that can trade automatically on your behalf. I encourage you to experiment changing/improving the algorithm on your own.

This example is also available on GitHub.

Posted on by Edward Atter 2

A Hands-On Introduction to Machine Learning

First, let me begin by setting some expectations. This is not a guide for the hardcore ML researchers out there. This is meant to be a practical introduction to machine learning that any computer scientist can follow, without much prior knowledge of the ML domain. I feel that there are many guides that focus solely on the academics of ML, but neglect to mention how simple it is to apply towards real life applications. Even naive approaches are often surprisingly effective.

To get started, we need to install scikit and other dependencies.

pip install numpy scipy scikit-learn

For simple implementations like we’ll see today, most of the challenge revolves around data prep. Our first step is to download the JSON training data from Kaggle. If you don’t already have an account, you’ll need to create one now. Once the account is created, visit the “What’s Cooking?” competition page and select the data tab to access the downloads.

Next, we need to format the data. A CSV format will be used, with each column representing a different ingredient and each row a single recipe. In ML lingo, the ingredients are features, the data we use as a basis for the predictions. Labels, the answer to each recipe, will be generated similarly. There’s nothing too novel with the code here, just some data wrangling.

Create a file called parser.py with the following code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#!/usr/bin/env python3

# Enable python2 compatability
from __future__ import print_function

import json

def main():
    # Define input/output file names
    train_file = "train.json"
    test_file = "test.json"
    train_file_out = "train.csv"
    test_file_out = "test.csv"
    train_file_out_labels = "train-labels.txt"
    json_data = None
    with open(train_file, 'r') as f:
        json_data = f.read()
    train_obj = json.loads(json_data)

    # Empty arrays to hold information
    labels_train = []
    labels_test = []
    # ingredients is defined as a set to prevent duplicates
    ingredients = set()

    # Generate corresponding labels and simultaneously make
    # exhaustive set of all posible cuisines (labels)
    with open(train_file_out_labels, 'w') as f:
        for recipe in train_obj:
            label = recipe["cuisine"]
            print(label, file=f)
            labels_train.append(label)
            for ingredient in recipe["ingredients"]:
                ingredients.add(ingredient)

    with open(test_file, 'r') as f:
        json_data = f.read()
    test_obj = json.loads(json_data)

    # The test file may introduce ingredients not included in training set
    # This ensures they're included
    for recipe in test_obj:
        for ingredient in recipe["ingredients"]:
            ingredients.add(ingredient)

    # Transform set to list to ensure iteration order is constant
    ingredients_list = list(ingredients)

    # Generate the CSV files
    generate_csv_for_each_recipe(ingredients_list, train_obj, train_file_out)
    generate_csv_for_each_recipe(ingredients_list, test_obj, test_file_out)

def generate_csv_for_each_recipe(ingredients_list, json_obj, output_file):
    """
    Creates an output csv file with each ingredient being a column
    and each recipe a row. 1 will represent the recipe contains the
    given ingredient if the recipe includes that incredient, else 0

    ingredients_list -- the full list of ingredients (without duplicates)
    json_obj -- the json object with recipes returned by json.loads
    output_file -- the name of the generated CSV file
    """
    # Loop thru each recipe
    with open(output_file, 'w') as f:
        for recipe in json_obj:
            rl = set()
            first = True
            s = ""
            for ingredient in recipe["ingredients"]:
                rl.add(ingredient)
            # This builds the csv row of ingredients for current recipe
            # Add 1 for ingredient if included in recipe; else 0
            for j in ingredients_list:
                # Don't prepend "," for first item
                if first != True:
                    s += ","  
                else:
                    first = False

                # Add 1 or 0 as explained above
                if j not in rl:
                    s += "0"
                else:
                    s += "1"
            print(s, file=f)

if __name__ == "__main__":
    main()

Create a new python script called train.py. Add some simple imports and variables that will prove useful later.

import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split

filename = "train.csv"
label_file = "train-labels.txt"
test_file = "test.csv"
prediction_output = "predictions.txt"

Load the data files generated previously with the parser script.

# Load the training features into a np array
features = np.loadtxt(filename, delimiter=',', dtype=np.uint8)
# Load the labels
with open(label_file) as f:
    labels = f.readlines()
# Strip any new line characters or extra spaces
labels = [x.strip() for x in labels]
# Convert to np array
labels = np.asarray(labels)

The next step is to split the training data into a training set and a testing set. This will allow us to estimate how well the classifier does on the “real” test data. Think about it, the testing data from Kaggle does not include the answers (labels). To have an easy way to see how well we’re doing, it’s necessary to split the data we do have answers for. It is not okay to test with the same features used in training — the accuracy will be artificially high. Scikit includes a handy feature to split the data for us.

# Split data up into training and test data
X_train, X_test, y_train, y_test = train_test_split(features, labels)

Instantiate and train the classifier with the split data set created from the last step. Selecting the best classifier is beyond the scope of this article, so we’ll just use the Logistic Regression classifier in this example, which performs pretty well. Scikit has an example testing different classifiers, if you want to explore.

print("Starting training...")
clf = LogisticRegression()
clf.fit(X_train, y_train)
score = clf.score(X_test, y_test)
print("Model has accuracy of " + str(score * 100) + "%")

Let’s use the same classifier to make predictions over the Kaggle test set, the one we don’t know the answers to. We’ll format this as simply one prediction per line.

print("Predicting over the Kaggle test set")
test_data = np.loadtxt(test_file, delimiter=',', dtype=np.uint8)
predictions = clf.predict(test_data)

with open(prediction_output, "w") as f:
    for prediction in predictions:
        print(prediction, file=f)

The last script we’ll write takes the predictions created in the last step and formats it in the specific way Kaggle expects. This will let us see how we performed against other solutions to the What’s Cooking Challenge.

Create a new script called kaggle.py. As usual, import the required modules and define a few helpful variables.

#!/usr/bin/env python3

from __future__ import print_function
import json

predict_file = "predictions.txt"
test_file = "test.json"
output_file = "kaggle.csv"

Read the prediction file

with open(predict_file) as f:
    labels = f.readlines()
labels = [x.strip() for x in labels]

Open the Kaggle test file and parse as JSON

with open(test_file, 'r') as f:
    json_data = f.read()
obj = json.loads(json_data)

Open the output file for writing and format as the Kaggle spec requires.

with open(output_file, "w") as out:
    # Print CSV headers
    print("id,cuisine", file=out)

    i = 0
    # Iterate through each recipe in the test file
    # Follow the spec in CSV format,
    # the recipe id followed by the cuisine prediction
    for recipe in obj:
        idx = recipe["id"]
        ingredient = labels[i]
        print(str(idx) + "," + ingredient, file=out)
        i += 1

To see how well you did, submit the generated kaggle.csv file to the Kaggle competition.

The complete code is available on GitHub.

For such a naive solution, we did pretty well here — successfully classifying over 77% of the recipes. There is, of course, room for improvement. It’s unlikely you’ll top the leader board with ready-made classifiers, but it’s close enough for many real-life problems and an excellent start to a future in machine learning.

Posted on by Edward Atter 0